Competitive analysis of the LRFU paging algorithm
1
| Edith Cohen |
 Haim Kaplan
Haim Kaplan
 Uri Zwick
Uri Zwick |
| AT&T Labs-Research |
School of Computer Science |
| 180 Park Avenue |
Tel-Aviv University |
| Florham Park, NJ 07932 USA |
Tel Aviv 69978, Israel |
| {edith}@research.att.com |
{haimk,zwick}@post.tau.ac.il |
April 22, 2001
Abstract:
We present a competitive analysis of the LRFU paging
algorithm, a hybrid of the LRU (Least Recently Used) and
LFU (Least Frequently Used) paging algorithms. We show
that the competitive ratio of LRFU is
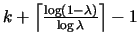
,
where
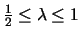
is the decay parameter used
by the LRFU algorithm, and
k is the size of the cache.
This supplies, in particular, the first natural paging
algorithms that are competitive but are not optimally
competitive, answering a question of Borodin and
El-Yaniv. Although LRFU, as it turns out, is not
optimally competitive, it is expected to behave well in
practice, as it combines
the benefits of both LRU and LFU.
Paging (cache replacement) algorithms have been extensively studied
and deployed. Two important applications are operating system
virtual memory paging and caching of Web content. The input to a
paging algorithm is a sequence of requests to different pages
and the size of the cache. The algorithm decides which page to
evict when a request arrives for a page which is not presently in the
cache and the cache is full. Often, the choice of a paging algorithm
can have a significant effect on performance.
Two important paging algorithms are Least Recently Used
( LRU) and Least Frequently Used ( LFU). LRU is
arguably the most commonly deployed in practice. One example application is
the popular Squid [#!Squid!#] Web caching software.2
When LRU has
to evict a page from its cache, it chooses to evict the least recently
requested page. LRU exploits temporal locality in request
sequences and the recency property which states that
recently requested objects are more likely to be requested next than objects
that have not been requested recently.
LFU is another policy that seems to perform well on Web request
sequences. LFU evicts the page in the cache that was requested the fewest
number of times. LFU comes in two flavors: in-cache LFU
which counts the number of times a page was requested since it entered the
cache, and perfect LFU which counts the total number of
requests made to the page since the start of the sequence. LFU
exploits the frequency property of request sequences which
states that pages that have been requested more times are more
likely to be requested again.
Recent studies (e.g. [#!BCFPS99!#]) comparing cache replacement algorithms
concluded that LRU and LFU exhibit comparable performance on Web
request sequences. In general, performance depends on the interplay
between the recency and frequency properties of the particular
sequence. Frequency seems to matter more for larger caches and
recency has a more pronounced impact with smaller cache sizes. Similar
behavior was observed for page request sequences in
operating systems [#!LCK99!#]. Motivated by these observations, Lee
et al. [#!LCK99!#] defined a spectrum of hybrid policies between
LRU and LFU. They named these policies LRFU ,
with
the parameter
,
with
the parameter 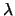 varying between
varying between 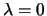 ( LRU) and
( LRU) and
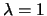 ( LFU). Their experiments based on simulations using
page requests generated by different application programs demonstrated
that the performance curve as a function of
( LFU). Their experiments based on simulations using
page requests generated by different application programs demonstrated
that the performance curve as a function of 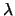 is smooth and
the dependence on
is smooth and
the dependence on 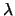 is bitonic: the miss-rate first decreases
and then increases as
is bitonic: the miss-rate first decreases
and then increases as 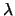 increases.
Thus typically LRFU
increases.
Thus typically LRFU outperforms at
least one of the endpoints and with the best choices of
outperforms at
least one of the endpoints and with the best choices of 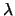 ,
LRFU
,
LRFU often outperforms both LRU and LFU. Their
results show that LRFU
often outperforms both LRU and LFU. Their
results show that LRFU does indeed provide a desirable
spectrum in terms of performance.
Competitive analysis is the leading theoretical tool for
analyzing the performance of paging algorithms [#!BoEl98!#]. A paging
algorithm A is said to have a competitive ratio of at most
c if on any request sequence, the number of misses of A is
at most c times the number of misses of the optimal offline algorithm,
plus some constant. A miss occurs when a requested page is not
in the cache. The competitive ratio of LRU and LFU demonstrates
both strengths and shortcomings of the ability of competitive analysis to
capture practical behavior. The LRU algorithm is optimally competitive.
That is, its competitive ratio of k is the best possible by any
deterministic paging algorithm (where k is the maximum number of pages that
can fit in the cache). On the other hand, the factor k obtained on
worst-case adversarial sequences is very far from the typical ratio on
actual sequences. Moreover, LFU, which performs comparably to LRU
on Web sequences, has an unbounded competitive ratio (is not
competitive). Practical sequences, as opposed to worst-case sequences,
typically exhibit the recency and frequency properties exploited by
LRU and LFU.
Interestingly, most natural deterministic paging algorithms fall in one
of these two categories: either they are optimally-competitive like
LRU, or they are noncompetitive like LFU. An open question posed
by Borodin and El-Yaniv [#!BoEl98!#] (open question 3.2 on page 43) is
the existence of a natural deterministic paging algorithm with a finite
but not optimal competitive ratio. It seems that most conceivable
hybrids of a non-competitive algorithm with an optimally-competitive
algorithms (such as partitioning the cache between the two policies) are
not competitive.
Our main contribution here is a tight competitive analysis of
LRFU
does indeed provide a desirable
spectrum in terms of performance.
Competitive analysis is the leading theoretical tool for
analyzing the performance of paging algorithms [#!BoEl98!#]. A paging
algorithm A is said to have a competitive ratio of at most
c if on any request sequence, the number of misses of A is
at most c times the number of misses of the optimal offline algorithm,
plus some constant. A miss occurs when a requested page is not
in the cache. The competitive ratio of LRU and LFU demonstrates
both strengths and shortcomings of the ability of competitive analysis to
capture practical behavior. The LRU algorithm is optimally competitive.
That is, its competitive ratio of k is the best possible by any
deterministic paging algorithm (where k is the maximum number of pages that
can fit in the cache). On the other hand, the factor k obtained on
worst-case adversarial sequences is very far from the typical ratio on
actual sequences. Moreover, LFU, which performs comparably to LRU
on Web sequences, has an unbounded competitive ratio (is not
competitive). Practical sequences, as opposed to worst-case sequences,
typically exhibit the recency and frequency properties exploited by
LRU and LFU.
Interestingly, most natural deterministic paging algorithms fall in one
of these two categories: either they are optimally-competitive like
LRU, or they are noncompetitive like LFU. An open question posed
by Borodin and El-Yaniv [#!BoEl98!#] (open question 3.2 on page 43) is
the existence of a natural deterministic paging algorithm with a finite
but not optimal competitive ratio. It seems that most conceivable
hybrids of a non-competitive algorithm with an optimally-competitive
algorithms (such as partitioning the cache between the two policies) are
not competitive.
Our main contribution here is a tight competitive analysis of
LRFU .
Our analysis reveals that as
.
Our analysis reveals that as 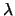 increases
we obtain all integral values between the competitive ratio of LRU
(k) and that of LFU (
increases
we obtain all integral values between the competitive ratio of LRU
(k) and that of LFU ( ). This solves the open problem
posed by Borodin and El-Yaniv. The full spectrum of values also
suggests that LRFU
). This solves the open problem
posed by Borodin and El-Yaniv. The full spectrum of values also
suggests that LRFU is the ``right'' hybrid of LRU and
LFU. In this sense the competitive analysis supports and complements
the experimental results.
The LRFU
is the ``right'' hybrid of LRU and
LFU. In this sense the competitive analysis supports and complements
the experimental results.
The LRFU paging policy, for
paging policy, for
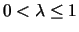 ,
is defined
as follows:
,
is defined
as follows:
- 1.
- Each page p currently in the cache has a value v(p)
associated with it.
- 2.
- Upon a request for a page q, the following operations are performed:
- (a)
- If a page has to be evicted to make room for q,
then the page with the smallest value is evicted. (Ties are broken
arbitrarily.) The new page q is temporarily given the value
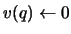 .
.
- (b)
- The values of the pages in the cache are updated as follows:
It follows that if a page p is in the cache at time t and if
the hits to this page, since it last entered the cache, were at times
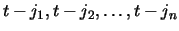 ,
then its value at time t is
,
then its value at time t is
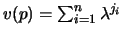 .
Note that the value v(p) of a page
is always smaller than
.
Note that the value v(p) of a page
is always smaller than
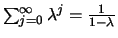 .
In particular, if
.
In particular, if
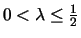 ,
then LRFU
,
then LRFU behaves just like LRU, since the most recent request time dominates the
value of the page (that is,
v(p1)<v(p2) if and only if the most recent
request to p1 occured before the most recent request to p2).
If
behaves just like LRU, since the most recent request time dominates the
value of the page (that is,
v(p1)<v(p2) if and only if the most recent
request to p1 occured before the most recent request to p2).
If 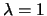 ,
then LRFU
,
then LRFU behaves just
like LFU. It is well known that LRU has an optimal competitive
ratio of k, while LFU is not competitive. We show that as
behaves just
like LFU. It is well known that LRU has an optimal competitive
ratio of k, while LFU is not competitive. We show that as 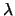 increases from
increases from
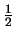 to 1, the competitive ratio of LRFU
to 1, the competitive ratio of LRFU increases from k to
increases from k to 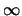 and assumes all possible integral
values in this range.
and assumes all possible integral
values in this range.
We obtain the following result:
Theorem 3.1
The competitive ratio of LRFU

for a cache of size
k,
where
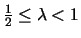
,
is
Another way of stating this result is as follows: the competitive ratio
of LRFU is
is 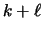 ,
where
,
where
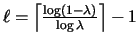 .
Note that
.
Note that
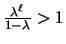 while
while
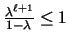 .
Thus,
.
Thus, 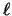 has the following
property: if p was not referenced in the last
has the following
property: if p was not referenced in the last 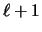 time units,
then v(p)<1.
time units,
then v(p)<1. 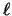 is the smallest number with this property.
Theorem
is the smallest number with this property.
Theorem ![[*]](/usr/common/latex2html/latex2html-98.1/icons.gif/cross_ref_motif.gif) follows from Lemmas
follows from Lemmas ![[*]](/usr/common/latex2html/latex2html-98.1/icons.gif/cross_ref_motif.gif) and
and ![[*]](/usr/common/latex2html/latex2html-98.1/icons.gif/cross_ref_motif.gif) that we obtain next.
that we obtain next.
Lemma 3.2
For every
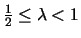
,
LRFU

is
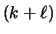
-competitive, where
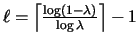
.
Figure:
LRFU incurs at most
incurs at most 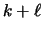 misses per k-phase.
misses per k-phase.
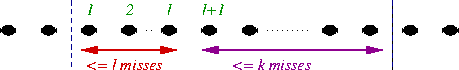 |
Proof:As in the classical analysis of LRU (see [#!BoEl98!#],
Chapter 3), we break the sequence of requests into k-phases.
A k-phase is a maximal contiguous block of requests in which at
most k different pages are requested. The first k-phase starts
at the beginning of the sequence and ends just before the (k+1)-st
distinct page is referenced. The second block begins immediately
after the first block and so on. It is easy to see that any caching
policy must incur, on average, at least one miss for each
k-phase. (More precisely, any caching policy must incur at least
one miss on each shifted k-phase, where a shifted
k-phase is a sequence of requests that begins with the second
request of an ordinary k-phase and ends with the first request of
the next ordinary k-phase.) To show that LRFU is
is
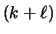 -competitive, we show that LRFU
-competitive, we show that LRFU incurs at most
incurs at most
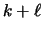 misses on each k-phase.
We first claim that under the LRFU
misses on each k-phase.
We first claim that under the LRFU policy, a page p that enters
the cache after the first
policy, a page p that enters
the cache after the first 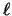 requests of a k-phase stays
in the cache until the end of the phase. This follows from the
interpretation of
requests of a k-phase stays
in the cache until the end of the phase. This follows from the
interpretation of 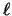 given after the statement of
Theorem
given after the statement of
Theorem ![[*]](/usr/common/latex2html/latex2html-98.1/icons.gif/cross_ref_motif.gif) . When p enters the cache, and is assigned the
value 1, the value v(q) of a page q that is currently in the
cache, but was not referenced yet in the current k-phase, must satisfy
v(q)<1. If a miss occurs in the k-phase after p enters the
cache, then there is at least one page q in the cache that was not
referenced yet in the k-phase. (If all k pages in the cache were
referenced in the current phase then a subsequent miss would end
the phase.) As v(q)<v(p), p will not be evicted.
It follows, therefore, that at most
. When p enters the cache, and is assigned the
value 1, the value v(q) of a page q that is currently in the
cache, but was not referenced yet in the current k-phase, must satisfy
v(q)<1. If a miss occurs in the k-phase after p enters the
cache, then there is at least one page q in the cache that was not
referenced yet in the k-phase. (If all k pages in the cache were
referenced in the current phase then a subsequent miss would end
the phase.) As v(q)<v(p), p will not be evicted.
It follows, therefore, that at most 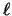 misses occur in the first
misses occur in the first
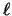 requests of each k-phase (at most one miss per request),
and at most k misses occur in the rest of the k-phase (at most
one miss per each page that enters the cache after the
requests of each k-phase (at most one miss per request),
and at most k misses occur in the rest of the k-phase (at most
one miss per each page that enters the cache after the 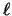 -th
request). (See Figure
-th
request). (See Figure ![[*]](/usr/common/latex2html/latex2html-98.1/icons.gif/cross_ref_motif.gif) .) This completes the proof of
the lemma.
.) This completes the proof of
the lemma.

Note that if
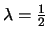 then
then  (i.e.,
(i.e.,  if and
only if p is the last page referenced), and Lemma
if and
only if p is the last page referenced), and Lemma ![[*]](/usr/common/latex2html/latex2html-98.1/icons.gif/cross_ref_motif.gif) states
that the competitive ratio of LRFU1/2= LRU
is k. Lemma
states
that the competitive ratio of LRFU1/2= LRU
is k. Lemma ![[*]](/usr/common/latex2html/latex2html-98.1/icons.gif/cross_ref_motif.gif) is therefore an extension of the classical
competitive analysis of the LRU policy.
An easy extension of Lemma
is therefore an extension of the classical
competitive analysis of the LRU policy.
An easy extension of Lemma ![[*]](/usr/common/latex2html/latex2html-98.1/icons.gif/cross_ref_motif.gif) is the following:
is the following:
Lemma 3.3
For every
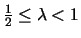
and
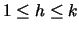
,
LRFU

with a cache of size
k is
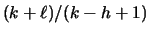
-competitive, where
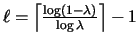
,
versus an
offline adversary that uses a cache of size
h.
Proof:Follows from the fact any algorithm that uses a cache of size h must
incur at least k-h+1 misses on each shifted k-phase.

We now show that the bound given in Lemma ![[*]](/usr/common/latex2html/latex2html-98.1/icons.gif/cross_ref_motif.gif) is tight.
is tight.
Lemma 3.4
For every
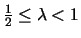
,
LRFU

is
at best 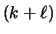
-competitive, where
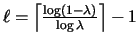
.
Proof:For every 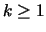 and
and
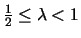 ,
we construct an
infinite sequence of requests such that the ratio between the number
of misses incurred by LRFU
,
we construct an
infinite sequence of requests such that the ratio between the number
of misses incurred by LRFU and the minimum possible number of
misses needed to serve the sequence approaches
and the minimum possible number of
misses needed to serve the sequence approaches 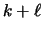 .
As in the
classical case of LRU, only k+1 distinct pages are needed for
this purpose.
Our sequences are again partitioned into k-phases. The state of
the cache at the end of each k-phase is isomorphic to the state of
the cache at the beginning of the phase. (This is explained below in
more detail.) We show that LRFU
.
As in the
classical case of LRU, only k+1 distinct pages are needed for
this purpose.
Our sequences are again partitioned into k-phases. The state of
the cache at the end of each k-phase is isomorphic to the state of
the cache at the beginning of the phase. (This is explained below in
more detail.) We show that LRFU incurs
incurs 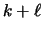 misses in each
phase. As there is a total of only k+1 pages, the sequence of
requests can be served with only one miss per k-phase. (At the first
miss of a phase, the optimal algorithm evicts the page that
is not going to be referenced in that phase.) The claim
of the lemma would thus follow.
Let L (for Large) be a sufficiently large number such that after L
consecutive requests to a page p we have
misses in each
phase. As there is a total of only k+1 pages, the sequence of
requests can be served with only one miss per k-phase. (At the first
miss of a phase, the optimal algorithm evicts the page that
is not going to be referenced in that phase.) The claim
of the lemma would thus follow.
Let L (for Large) be a sufficiently large number such that after L
consecutive requests to a page p we have
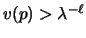 and
v(q)<1 for any page q such that
and
v(q)<1 for any page q such that 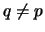 .
Such
a number exists as by the definition of
.
Such
a number exists as by the definition of 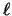 we have
we have
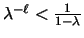 .
The first initializing k-phase is composed of the following page
requests:
.
The first initializing k-phase is composed of the following page
requests:
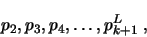
where piL
stands for L consecutive requests of the page pi. At the end
of this phase, the pages in the cache, in decreasing order of
their values, are
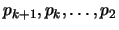 ,
and their values satisfy
,
and their values satisfy
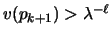 and v(pi)<1, for
and v(pi)<1, for
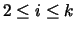 .
The second phase is now composed of the following page requests:
.
The second phase is now composed of the following page requests:
where the parentheses
around the indices indicate that they should be interpreted
modulo k (i.e.,
p(k+1)=p1, and more generally
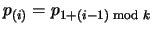 .
What happens to the cache when this sequence of requests is
served? At the beginning of the phase
.
What happens to the cache when this sequence of requests is
served? At the beginning of the phase
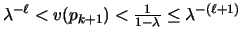 (the last
inequality follows from the definition of
(the last
inequality follows from the definition of 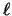 ). Thus,
during the first
). Thus,
during the first 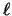 requests of the phase, page pk+1
still has the largest value among all the pages of the cache, and
the page entering the cache becomes the page with the
second largest value. The page evicted is always
the next page requested, and thus each request causes a miss.
When the
requests of the phase, page pk+1
still has the largest value among all the pages of the cache, and
the page entering the cache becomes the page with the
second largest value. The page evicted is always
the next page requested, and thus each request causes a miss.
When the 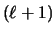 -st request of the phase is served, the value
of
v(pk+1) drops below 1. The page entering the cache now
becomes the page with the largest weight. The rank of
pk+1 in the cache decreases by 1 at each step. The page
evicted is again the next page requested and thus each request
still causes a miss. While serving
the request for
-st request of the phase is served, the value
of
v(pk+1) drops below 1. The page entering the cache now
becomes the page with the largest weight. The rank of
pk+1 in the cache decreases by 1 at each step. The page
evicted is again the next page requested and thus each request
still causes a miss. While serving
the request for
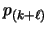 ,
page pk+1 is finally
evicted from the cache.
Overall, there are
,
page pk+1 is finally
evicted from the cache.
Overall, there are 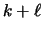 misses in this phase. The content of
the cache during such a phase is depicted in
Figure
misses in this phase. The content of
the cache during such a phase is depicted in
Figure ![[*]](/usr/common/latex2html/latex2html-98.1/icons.gif/cross_ref_motif.gif) . (In the figure, it is assumed, for
simplicity, that
. (In the figure, it is assumed, for
simplicity, that  .
The argument given above does not rely on
this assumption.)
.
The argument given above does not rely on
this assumption.)
Figure:
A typical phase of the worst-case sequence for
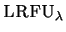
 |
Now, the state of cache at the end of the second phase is similar
to its state at the end of the first phase. One page, namely
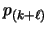 ,
has value larger than
,
has value larger than
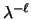 ,
while all
other pages have values that are less than 1. We can therefore use
a sequence of requests similar to the one used in the second
state, and again create a k-phase in which LRFU
,
while all
other pages have values that are less than 1. We can therefore use
a sequence of requests similar to the one used in the second
state, and again create a k-phase in which LRFU incurs
incurs
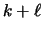 misses. This process can be repeated indefinitely,
resulting in the promised infinite sequence of requests.
misses. This process can be repeated indefinitely,
resulting in the promised infinite sequence of requests.

The plain LRU, LFU, and LRFU
 algorithms are designed for
pages with equal sizes and miss costs.
Web objects, however, vary significantly in both size and cost of a miss.
This motivated the development of cache replacement algorithms that account
for varying page sizes and fetching
costs [#!Irani97!#,#!Young2!#,#!CaoIrani!#,#!CoKa99a!#]. Experiments showed that
the optimally-competitive Landlord algorithm performs well on Web
caching sequences [#!Young2!#,#!CaoIrani!#]. Other experiments, however,
show that it can be outperformed by perfect LFU [#!BCFPS99!#].
A natural open problem is thus to extend our results to this
more general model. That is, develop natural hybrid policies of
Landlord and ``weighted'' LFU.
algorithms are designed for
pages with equal sizes and miss costs.
Web objects, however, vary significantly in both size and cost of a miss.
This motivated the development of cache replacement algorithms that account
for varying page sizes and fetching
costs [#!Irani97!#,#!Young2!#,#!CaoIrani!#,#!CoKa99a!#]. Experiments showed that
the optimally-competitive Landlord algorithm performs well on Web
caching sequences [#!Young2!#,#!CaoIrani!#]. Other experiments, however,
show that it can be outperformed by perfect LFU [#!BCFPS99!#].
A natural open problem is thus to extend our results to this
more general model. That is, develop natural hybrid policies of
Landlord and ``weighted'' LFU.
No References!
Competitive analysis of the LRFU paging algorithm
1
This document was generated using the
LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)
Copyright © 1993, 1994, 1995, 1996, 1997,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 1 -no_navigation -show_section_numbers lrfu-html.
The translation was initiated by Edith Cohen on 2001-08-27
Edith Cohen
2001-08-27
![]() Haim Kaplan
Haim Kaplan
![]() Uri Zwick
Uri Zwick 
![]() ,
then its value at time t is
,
then its value at time t is
![]() .
Note that the value v(p) of a page
is always smaller than
.
Note that the value v(p) of a page
is always smaller than
![]() .
In particular, if
.
In particular, if
![]() ,
then LRFU
,
then LRFU![]() behaves just like LRU, since the most recent request time dominates the
value of the page (that is,
v(p1)<v(p2) if and only if the most recent
request to p1 occured before the most recent request to p2).
If
behaves just like LRU, since the most recent request time dominates the
value of the page (that is,
v(p1)<v(p2) if and only if the most recent
request to p1 occured before the most recent request to p2).
If ![]() ,
then LRFU
,
then LRFU![]() behaves just
like LFU. It is well known that LRU has an optimal competitive
ratio of k, while LFU is not competitive. We show that as
behaves just
like LFU. It is well known that LRU has an optimal competitive
ratio of k, while LFU is not competitive. We show that as ![]() increases from
increases from
![]() to 1, the competitive ratio of LRFU
to 1, the competitive ratio of LRFU![]() increases from k to
increases from k to ![]() and assumes all possible integral
values in this range.
and assumes all possible integral
values in this range.
![]() is
is
![]() -competitive, we show that LRFU
-competitive, we show that LRFU![]() incurs at most
incurs at most
![]() misses on each k-phase.
We first claim that under the LRFU
misses on each k-phase.
We first claim that under the LRFU![]() policy, a page p that enters
the cache after the first
policy, a page p that enters
the cache after the first ![]() requests of a k-phase stays
in the cache until the end of the phase. This follows from the
interpretation of
requests of a k-phase stays
in the cache until the end of the phase. This follows from the
interpretation of ![]() given after the statement of
Theorem
given after the statement of
Theorem ![]() . When p enters the cache, and is assigned the
value 1, the value v(q) of a page q that is currently in the
cache, but was not referenced yet in the current k-phase, must satisfy
v(q)<1. If a miss occurs in the k-phase after p enters the
cache, then there is at least one page q in the cache that was not
referenced yet in the k-phase. (If all k pages in the cache were
referenced in the current phase then a subsequent miss would end
the phase.) As v(q)<v(p), p will not be evicted.
It follows, therefore, that at most
. When p enters the cache, and is assigned the
value 1, the value v(q) of a page q that is currently in the
cache, but was not referenced yet in the current k-phase, must satisfy
v(q)<1. If a miss occurs in the k-phase after p enters the
cache, then there is at least one page q in the cache that was not
referenced yet in the k-phase. (If all k pages in the cache were
referenced in the current phase then a subsequent miss would end
the phase.) As v(q)<v(p), p will not be evicted.
It follows, therefore, that at most ![]() misses occur in the first
misses occur in the first
![]() requests of each k-phase (at most one miss per request),
and at most k misses occur in the rest of the k-phase (at most
one miss per each page that enters the cache after the
requests of each k-phase (at most one miss per request),
and at most k misses occur in the rest of the k-phase (at most
one miss per each page that enters the cache after the ![]() -th
request). (See Figure
-th
request). (See Figure ![]() .) This completes the proof of
the lemma.
.) This completes the proof of
the lemma.
![]()
![]() then
then ![]() (i.e.,
(i.e., ![]() if and
only if p is the last page referenced), and Lemma
if and
only if p is the last page referenced), and Lemma ![]() states
that the competitive ratio of LRFU1/2= LRU
is k. Lemma
states
that the competitive ratio of LRFU1/2= LRU
is k. Lemma ![]() is therefore an extension of the classical
competitive analysis of the LRU policy.
An easy extension of Lemma
is therefore an extension of the classical
competitive analysis of the LRU policy.
An easy extension of Lemma ![]() is the following:
is the following:
![]()
![]() and
and
![]() ,
we construct an
infinite sequence of requests such that the ratio between the number
of misses incurred by LRFU
,
we construct an
infinite sequence of requests such that the ratio between the number
of misses incurred by LRFU![]() and the minimum possible number of
misses needed to serve the sequence approaches
and the minimum possible number of
misses needed to serve the sequence approaches ![]() .
As in the
classical case of LRU, only k+1 distinct pages are needed for
this purpose.
Our sequences are again partitioned into k-phases. The state of
the cache at the end of each k-phase is isomorphic to the state of
the cache at the beginning of the phase. (This is explained below in
more detail.) We show that LRFU
.
As in the
classical case of LRU, only k+1 distinct pages are needed for
this purpose.
Our sequences are again partitioned into k-phases. The state of
the cache at the end of each k-phase is isomorphic to the state of
the cache at the beginning of the phase. (This is explained below in
more detail.) We show that LRFU![]() incurs
incurs ![]() misses in each
phase. As there is a total of only k+1 pages, the sequence of
requests can be served with only one miss per k-phase. (At the first
miss of a phase, the optimal algorithm evicts the page that
is not going to be referenced in that phase.) The claim
of the lemma would thus follow.
Let L (for Large) be a sufficiently large number such that after L
consecutive requests to a page p we have
misses in each
phase. As there is a total of only k+1 pages, the sequence of
requests can be served with only one miss per k-phase. (At the first
miss of a phase, the optimal algorithm evicts the page that
is not going to be referenced in that phase.) The claim
of the lemma would thus follow.
Let L (for Large) be a sufficiently large number such that after L
consecutive requests to a page p we have
![]() and
v(q)<1 for any page q such that
and
v(q)<1 for any page q such that ![]() .
Such
a number exists as by the definition of
.
Such
a number exists as by the definition of ![]() we have
we have
![]() .
The first initializing k-phase is composed of the following page
requests:
.
The first initializing k-phase is composed of the following page
requests: